余弦定理は「いつ使うか」が9割！暗記に頼らず図解でマスターする決定版ガイド

「公式が長くて覚えにくい」「正弦定理とどっちを使えばいいのか分からない」……。高校数学の三角比で、多くの受験生が最初にぶつかる壁が余弦定理（よげんていり）です。

しかし、余弦定理の本質は、中学で習った「三平方の定理」を少しだけパワーアップさせたものに過ぎません。この記事では、20年間数学を教えてきた専門家の視点から、余弦定理を丸暗記に頼らず、図形を見た瞬間に「あ、ここは余弦定理だ！」と判断できるようになるための「パターン認識」のコツを徹底解説します。

[著者情報]

佐藤健一（さとうけんいち）
数学教育コンサルタント。大手予備校で20年以上、高校数学の指導に従事。「公式の背景にある論理」を可視化する指導法に定評があり、これまでに5,000人以上の志望校合格をサポート。著書に『図解でわかる！数学の思考回路』など。

[著者情報]

余弦定理の正体とは？三平方の定理を「どんな三角形」にも広げた最強の武器
【UVP】もう迷わない！正弦定理と余弦定理の「使い分け」をパターンで完全攻略
余弦定理の計算ミスをゼロにする！3つのステップと「角度」を求める変形コツ
1. 余弦定理の「基本形」と「変形版」の使い分け
余弦定理に関するよくある質問（FAQ）
まとめ：余弦定理を「一生モノの道具」にするために

余弦定理の正体とは？三平方の定理を「どんな三角形」にも広げた最強の武器

[セクションの目的]: 余弦定理の定義を、既知の知識（三平方の定理）と結びつけて解説し、心理的ハードルを下げます。

余弦定理を「全く新しい、複雑な公式」だと思っていませんか？実は、余弦定理は「三平方の定理」を、直角三角形以外のあらゆる三角形でも使えるように拡張したものです。

まずは、余弦定理の公式を再確認しましょう。三角形ABCにおいて、角A, B, Cの向かい合う辺をa, b, cとすると、以下の関係が成り立ちます。

余弦定理の基本公式
$a^2 = b^2 + c^2 – 2bc \cos A$

この式をよく見てください。もし角Aが90度（直角）だった場合、$\cos 90^\circ = 0$ となるため、後ろの「$- 2bc \cos A$」の部分が消えて、$a^2 = b^2 + c^2$ という三平方の定理そのものになります。つまり、余弦定理とは「直角じゃないから三平方の定理が使えない！という時のための補正付き三平方の定理」なのです。

✍️ 専門家の経験からの一言アドバイス

【結論】: 公式を覚えるときは、まず「$a^2 = b^2 + c^2$」という三平方の定理の形を書き、その後に「$-2bc \cos A$」という補正パーツを付け足すと考えると、符号のミスが激減します。

なぜなら、この「補正パーツ」の意味を理解せずに丸暗記しようとするから、試験中にプラスかマイナスか混乱してしまうのです。余弦定理は三平方の定理の進化系である、というイメージを常に持っておきましょう。

【UVP】もう迷わない！正弦定理と余弦定理の「使い分け」をパターンで完全攻略

[セクションの目的]: 競合記事が曖昧にしがちな「正弦定理との使い分け」を、独自の判断基準（UVP）で明確に示します。

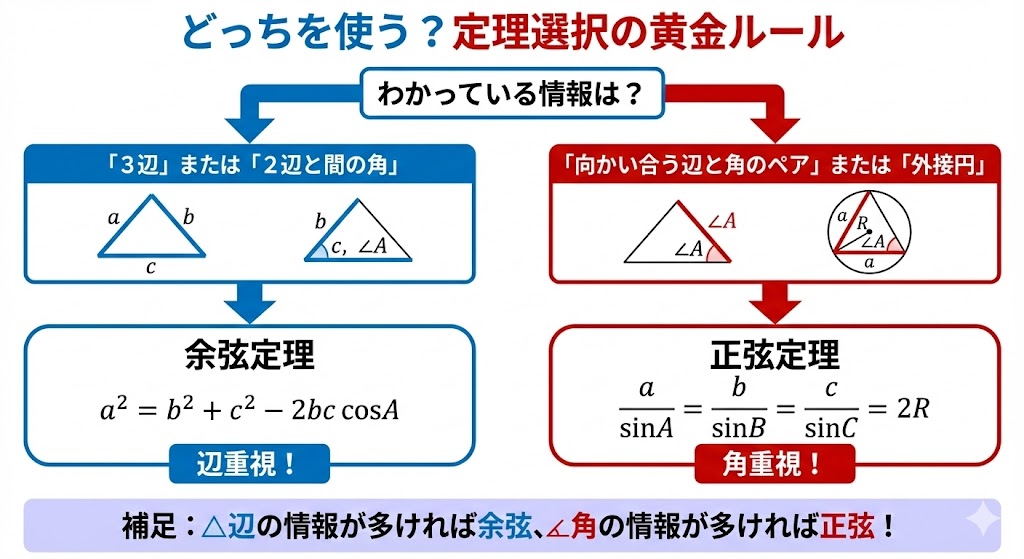
テスト中に最も多い悩みが「正弦定理と余弦定理、どっちを使えばいいの？」というものです。結論から言いましょう。余弦定理を使うべき場面は、図形の中に「辺の情報が多いとき」です。

具体的には、以下の2つのパターンに当てはまれば、迷わず余弦定理を選択してください。

「2辺とその間の角」がわかっているとき（残りの1辺を求めたい）
「3辺」がすべてわかっているとき（好きな角の大きさを求めたい）

逆に、正弦定理は「向かい合う辺と角のペア」が2組作れるときや、外接円の半径が絡むときに使います。

余弦定理の計算ミスをゼロにする！3つのステップと「角度」を求める変形コツ

[セクションの目的]: 実践的な計算手順と、角度を求める際の変形公式（エンティティの関係性）を解説します。

余弦定理は式が長いため、代入ミスや計算ミスが多発します。特に、角の大きさを求めるために公式を変形する際、多くの受験生が躓きます。

角度を求めたいときは、基本の公式をあらかじめ変形した「余弦定理の変形版」を使いましょう。

角度を求めるための余弦定理（変形版）
$\cos A = \frac{b^2 + c^2 – a^2}{2bc}$

この変形版公式を使いこなすための3ステップを紹介します。

ターゲットの角を決める: 求めたい角をAとします。
「挟んでいる2辺」を分母と分子の先頭に置く: 角Aを挟んでいる辺bと辺cを、$2bc$（分母）と $b^2 + c^2$（分子）に配置します。
「向かい合う辺」を最後に引く: 角Aの向かい側にある辺aを、$-a^2$ として分子の最後に引きます。

余弦定理の変形版において、分子の最後に引かれるのは必ず「求めたい角の向かい側にある辺」です。この関係性を意識するだけで、代入する場所を間違えることはなくなります。

余弦定理の「基本形」と「変形版」の使い分け

項目	基本形 ($a^2 = \dots$)	変形版 ($\cos A = \dots$)
目的	残りの「辺」を求めたいとき	特定の「角」を求めたいとき
既知の情報	2辺とその間の角	3辺すべて
計算の注意点	$\cos$ の値（特に鈍角）の符号	分子の引き算の順番

余弦定理に関するよくある質問（FAQ）

[セクションの目的]: 読者が抱きやすい補足的な疑問に答え、理解を深めます。

Q1. $\cos$ がマイナスになることがあるのですが、計算ミスですか？
A1. いいえ、正しい結果です。角Aが鈍角（90度より大きい）の場合、$\cos A$ の値は必ずマイナスになります。例えば $\cos 120^\circ = -1/2$ です。このマイナスを忘れると、辺の長さが異常に短くなってしまうので注意しましょう。

Q2. 余弦定理を証明できないと入試で不利ですか？
A2. 公式を使えることが最優先ですが、難関大を目指すなら証明（座標平面や垂線を用いた方法）も一度は目を通しておくべきです。余弦定理の証明プロセスには、図形問題を解くためのエッセンスが詰まっているからです。