数学の授業で突然登場する「$| \quad |$」という記号。マイナスを取るだけだと思っていたら、文字式の計算で急に難しく感じてしまったという方も多いのではないでしょうか。
結論から言えば、絶対値とは「数直線上で、ある数から原点(0)までの距離」のことです。
この記事では、数学教育アドバイザーの視点から、絶対値の根本的な意味、計算のルール、そして多くの学生が躓きやすい「文字を含む絶対値記号の外し方」について、図解を交えて徹底的に解説します。
✍️ 専門家の経験からの一言アドバイス:数学教育アドバイザー「カズ先生」
名前: 佐藤 カズキ(さとう かずき)
肩書き: 数学教育アドバイザー・元予備校講師(キャリア15年)
専門領域: 中高数学の概念理解、苦手克服カリキュラム作成
✍️ 専門家の経験からの一言アドバイス
【結論】: 絶対値を「マイナスを取る魔法」だと思わないでください。「絶対値は常に0以上の距離である」というイメージを強く持つことが重要です。
なぜなら、高校数学で登場する $|a| = -a$ ($a < 0$ のとき)という式を見たときに、「絶対値なのにマイナスがつくのはおかしい!」と混乱してしまうからです。このマイナスは「負の数 $a$ を正に変えるためのマイナス」です。この本質を理解すれば、文字式の絶対値も怖くありません。
1. 絶対値の根本的な意味:数直線上の「距離」
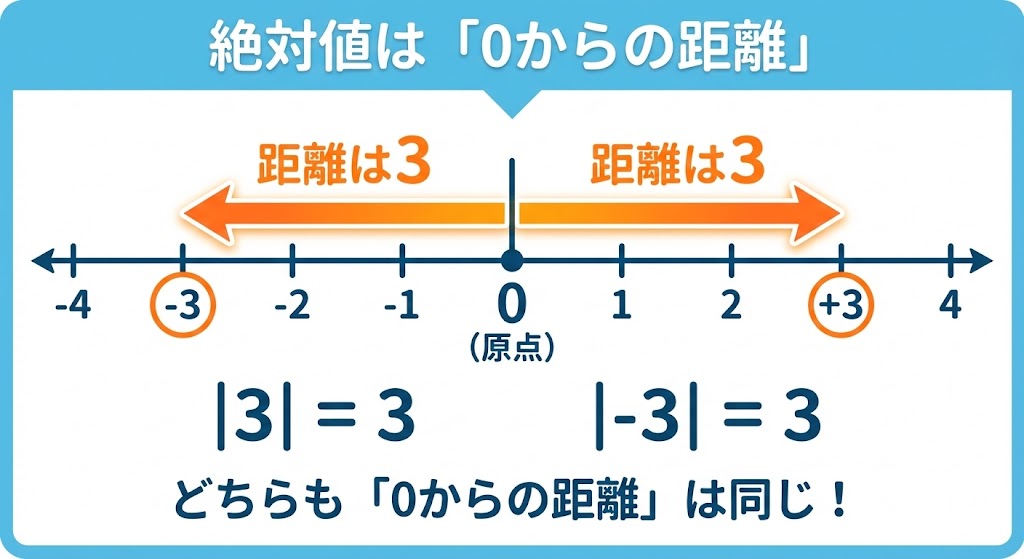
絶対値とは、数直線上で「原点(0)からどれだけ離れているか」という距離を表す概念です。
なぜマイナスが消えるのか?
日常会話でも「駅から家までマイナス500メートルです」とは言いませんよね。方向が右(プラス)であっても左(マイナス)であっても、離れている長さ(距離)は常に正の数になります。数学の世界でも、この「純粋な長さ」を取り出したものが絶対値なのです。
数値と絶対値の対応例
| 数値 | 記号での表記 | 絶対値(結果) | 意味(0からの距離) |
|---|---|---|---|
| 5 | $ | 5 | $ |
| -3 | $ | -3 | $ |
| 0 | $ | 0 | $ |
| -1.5 | $ | -1.5 | $ |
2. 【重要】絶対値記号の外し方(文字式の場合)
絶対値の計算で最も重要なのが、絶対値記号 $| \quad |$ を外すときのルールです。中身が具体的な数字なら簡単ですが、文字 $a$ になった瞬間に注意が必要になります。
絶対値記号の外し方の公式
絶対値記号の中身が「0以上」か「負」かによって、外し方は2パターンに分かれます。
- 中身が0以上のとき:そのまま外す
$|a| = a$ ($a \geqq 0$ のとき) - 中身が負のとき:マイナスをつけて外す
$|a| = -a$ ($a < 0$ のとき)
なぜ負のときはマイナスをつけるのか?
例えば $a = -5$ のときを考えてみましょう。
$|-5|$ は $5$ にならなければなりません。これを文字 $a$ を使って表すと、$-(-5)$、つまり $-a$ とすることで、結果を正の数(5)にしているのです。「マイナスをつけることで、負の数を正に変えている」と理解しましょう。
3. 2点間の距離としての絶対値
絶対値は、原点からの距離だけでなく、「2つの地点がどれだけ離れているか」を求める際にも使われます。
2点間の距離の公式
数直線上の2点 $A(a)$ と $B(b)$ の間の距離は、以下の式で表せます。
距離 $AB = |b – a|$
どちらの数から引いても、絶対値記号をつければ必ず正の距離が求められます。
(例:3と8の距離は、 $|8 – 3| = 5$ でも $|3 – 8| = |-5| = 5$ でも同じ結果になります)
絶対値は、物理学や統計学においても「誤差」や「変動の大きさ」を測るための不可欠な道具として使われています。
出典: [文部科学省]「高等学校学習指導要領(平成30年告示)解説 数学編」 – 2024年参照
4. FAQ:絶対値に関するよくある疑問
Q. 絶対値がマイナスになることはありますか?
A. いいえ、絶対値の結果がマイナスになることは絶対にありません。 絶対値は「距離」を表すため、必ず0以上の値になります。もし計算結果がマイナスになったら、どこかで符号のミスをしているサインです。
Q. $|x – 2| = 3$ のような方程式はどう解けばいいですか?
A. 「$x – 2$ という地点が、0から3離れている」と考えます。
つまり、 $x – 2 = 3$ または $x – 2 = -3$ の2つのケースを解けばOKです。
答えは $x = 5, -1$ となります。
まとめ:絶対値は「距離」のイメージで攻略
絶対値の理解を深めるポイントを振り返ります。
- 絶対値は「数直線上の0からの距離」である。
- 距離なので、結果は必ず0以上になる。
- 文字式の絶対値を外すときは、中身の符号(プラスかマイナスか)で場合分けする。
- 中身がマイナスのときは、マイナスをつけて正の数に変えて外す。
絶対値は、この先の「絶対値を含む関数」や「不等式」の基礎となる非常に重要な単元です。まずは「0からの距離」というイメージを大切に、基本問題を繰り返し解いてみてください。
参考文献リスト
- 文部科学省「中学校学習指導要領(平成29年告示)解説 数学編」
- 啓林館「数学シリーズ」教科書ガイド
- 数研出版「チャート式 基礎からの数学I+A」
[著者情報]
佐藤 カズキ: 数学教育アドバイザー。15年間にわたり予備校で中高生を指導。現在はオンラインでの学習支援や、数学の苦手意識をなくすための教材開発を行っている。趣味は数式を使ったプログラミング。

コメント